Interaction picture
| Quantum mechanics |
|---|
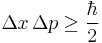 |
| Introduction Glossary · History |
|
Background
|
|
Fundamental concepts
|
|
Formulations
|
|
Equations
|
|
Advanced topics
|
|
Scientists
Bell · Bohm · Bohr · Born · Bose
de Broglie · Dirac · Ehrenfest Everett · Feynman · Heisenberg Jordan · Kramers · von Neumann Pauli · Planck · Schrödinger Sommerfeld · Wien · Wigner |
In quantum mechanics, the Interaction picture (or Dirac picture) is an intermediate between the Schrödinger picture and the Heisenberg picture. Whereas in the other two pictures either the state vector or the operators carry time dependence, in the interaction picture both carry part of the time dependence of observables.
Equations that include operators acting at different times, which hold in the interaction picture, don't necessarily hold in the Schrödinger or the Heisenberg picture. This is because time-dependent unitary transformations relate operators in one picture to the analogous operators in the others. Not all textbooks and articles make explicit which picture each operator comes from, which can lead to confusion and mistakes.
Contents |
Definition
Operators and state vectors in the interaction picture are related by a change of basis (unitary transformation) to those same operators and state vectors in the Schrödinger picture.
To switch into the interaction picture, we divide the Schrödinger picture Hamiltonian into two parts, 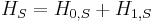 . (Any possible choice of parts will yield a valid interaction picture; but in order for the interaction picture to be useful in simplifying the analysis of a problem, the parts will typically be chosen so that
. (Any possible choice of parts will yield a valid interaction picture; but in order for the interaction picture to be useful in simplifying the analysis of a problem, the parts will typically be chosen so that 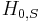 is well understood and exactly solvable, and
is well understood and exactly solvable, and 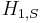 contains some harder-to-analyze perturbation to this system.)
contains some harder-to-analyze perturbation to this system.)
If the Hamiltonian has explicit time-dependence (for example, if the quantum system interacts with an applied external electric field that varies in time), it will usually be advantageous to include the explicitly time-dependent terms with 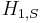 , leaving
, leaving 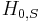 time-independent. We will proceed assuming that this is the case. (If there is a context in which it makes sense to have
time-independent. We will proceed assuming that this is the case. (If there is a context in which it makes sense to have 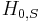 be time-dependent, then one can proceed by replacing
be time-dependent, then one can proceed by replacing 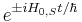 by the corresponding time-evolution operator in the definitions below.)
by the corresponding time-evolution operator in the definitions below.)
State vectors
A state vector in the interaction picture is defined as[1]
(where 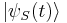 is the same state vector in the Schrödinger picture.)
is the same state vector in the Schrödinger picture.)
Operators
An operator in the interaction picture is defined as
(Note that the 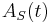 will typically not depend on t, and can be rewritten as just
will typically not depend on t, and can be rewritten as just 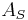 . It only depends on t if the operator has "explicit time dependence", for example due to its dependence on an applied, external, time-varying electric field.)
. It only depends on t if the operator has "explicit time dependence", for example due to its dependence on an applied, external, time-varying electric field.)
Hamiltonian operator
For the operator 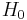 itself, the interaction picture and Schrödinger picture are the same:
itself, the interaction picture and Schrödinger picture are the same:
(this can be proved using the fact that operators commute with differentiable functions of themselves.) This particular operator can thus be called 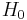 with no ambiguity.
with no ambiguity.
For the perturbation Hamiltonian 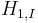 , we have:
, we have:
where the interaction picture perturbation Hamiltonian becomes a time-dependent Hamiltonian (unless ![[H_{1,s},H_{0,s}]=0](/2012-wikipedia_en_all_nopic_01_2012/I/8d904e7bd767901c93ab4befb0f7ba40.png) ).
).
It is possible to obtain the interaction picture for a time-dependent Hamiltonian 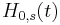 as well but the exponentials need to be replaced by the unitary propagator for the evolution due to
as well but the exponentials need to be replaced by the unitary propagator for the evolution due to 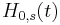 or more explicitly with a time-ordered exponential integral.
or more explicitly with a time-ordered exponential integral.
Density matrix
The density matrix can be shown to transform to the interaction picture in the same way as any other operator. In particular, let 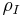 and
and 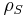 be the density matrix in the interaction picture and the Schrödinger picture, respectively. If there is probability
be the density matrix in the interaction picture and the Schrödinger picture, respectively. If there is probability 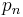 to be in the physical state
to be in the physical state 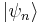 , then
, then
Time-evolution equations in the interaction picture
Time-evolution of states
Transforming the Schrödinger equation into the interaction picture gives:
This equation is referred to as the Schwinger-Tomonaga equation.
Time-evolution of operators
If the operator 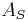 is time independent (i.e., does not have "explicit time dependence"; see above), then the corresponding time evolution for
is time independent (i.e., does not have "explicit time dependence"; see above), then the corresponding time evolution for 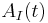 is given by:
is given by:
In the interaction picture the operators evolve in time like the operators in the Heisenberg picture with the Hamiltonian 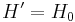 .
.
Time-evolution of the density matrix
Transforming the Schwinger-Tomonaga equation into the language of the density matrix (or equivalently, transforming the von Neumann equation into the interaction picture) gives:
Use of interaction picture
The purpose of the interaction picture is to shunt all the time dependence due to H0 onto the operators, leaving only H1, I affecting the time-dependence of the state vectors.
The interaction picture is convenient when considering the effect of a small interaction term, H1, S, being added to the Hamiltonian of a solved system, H0, S. By switching into the interaction picture, you can use time-dependent perturbation theory to find the effect of H1, I.
References
- Townsend, John S. (2000). A Modern Approach to Quantum Mechanics, 2nd ed.. Sausalito, CA: University Science Books. ISBN 1-891389-13-0.
- ^ The Interaction Picture, lecture notes from New York University
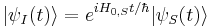
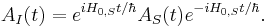
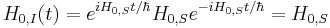
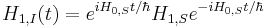
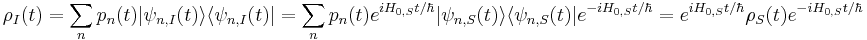
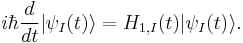
![i\hbar\frac{d}{dt}A_I(t)=\left[A_I(t),H_0\right].\;](/2012-wikipedia_en_all_nopic_01_2012/I/daa22f10c7652ae07bca7b2e7ec9c8d9.png)
![i\hbar \frac{d}{dt} \rho_I(t) = \left[ H_{1,I}(t), \rho_I(t)\right].](/2012-wikipedia_en_all_nopic_01_2012/I/3e7db1e7e324071a47e2fdda92abb453.png)